본 포스트에서는 클러스터링 기반 이상감지 모델 중 DBSCAN에 대해 간략하게 설명하도록 하겠습니다.

작성자 : 박상민 - (주)인스페이스 미래기술실 연구원

본 포스트는 약 4개월간 이상감지(Anomaly Detection)를 연구하게 되면서 공부했던 것, 알아낸 것, 찾아봤던 자료, 구현체, 결과물 등을 정리해서 공유하는 글 입니다.

주관적인 내용이 포함되어 있으니 이해해주시기 바랍니다. 항공우주분야의 이상감지를 연구해왔기 때문에 글의 내용도 도메인에 밀접한 내용이 있으니 참고하시면 좋을 것 같습니다.

클러스터링 기반 이상감지 모델

클러스터링 방식은 특성이 비슷한 데이터들을 군집화하는 비지도학습 방식의 머신러닝 기법입니다. 키가 비슷한 사람들을 군집해주거나, 가까운 지역에 있는 사람들을 묶어주는 것 등에 사용될 수 있습니다.

클러스터링 알고리즘은 다양합니다. K-means, DBSCAN, 계층적 군집화(Hiarchical Clustering)등이 있으며, 각각 알고리즘에 따라 성능이나 속도에 차이가 있습니다.

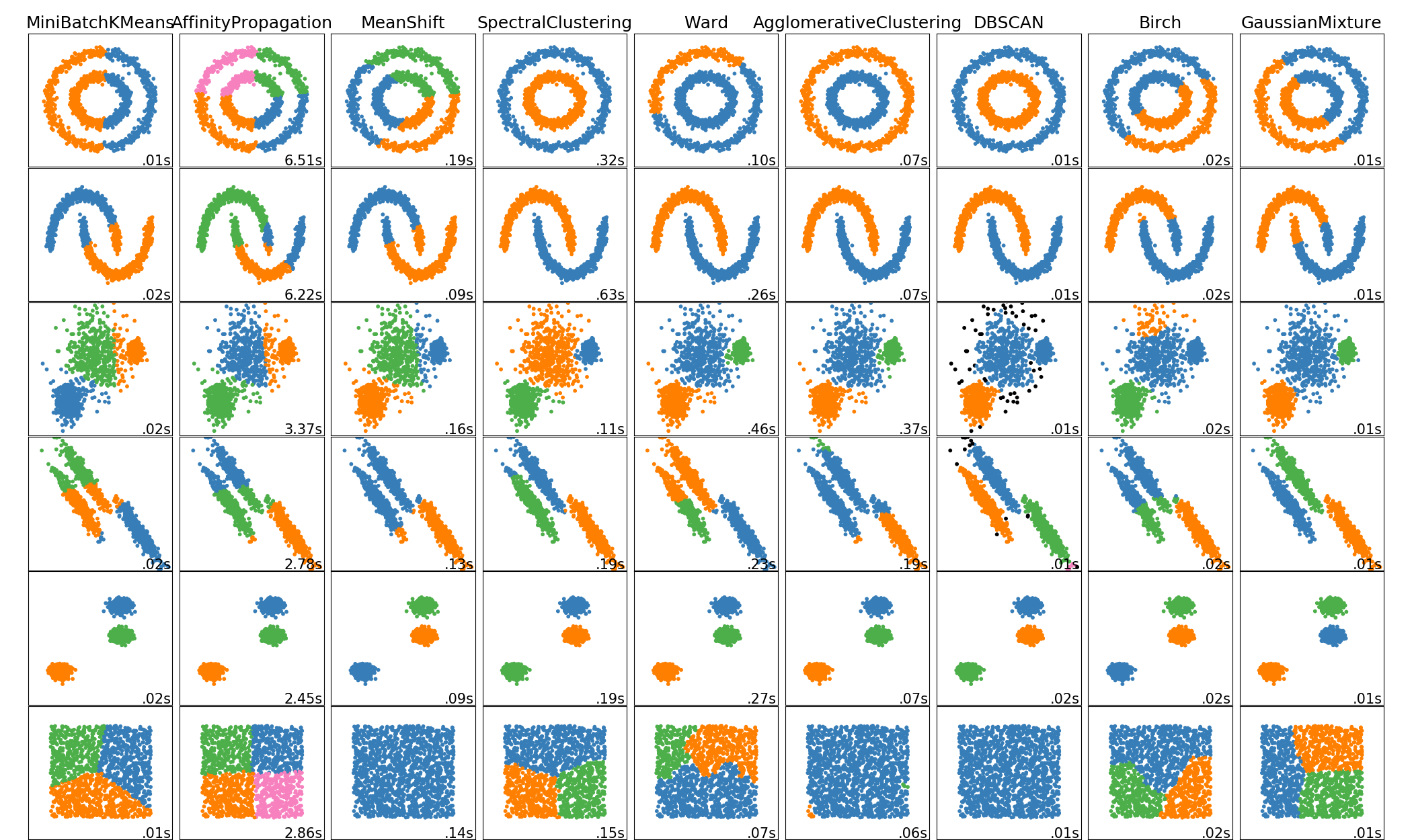
아래 사진은 scikit-learn에 나와있는 각 클러스터링 알고리즘의 성능을 비교하여 보여주고있습니다. 대부분의 클러스터링 알고리즘은 scikit-learn에서 제공해주고 있습니다. 참고하시면 좋을 것 같습니다. 출처

DBSCAN(ensity-based spatial clustering of applications with noise)

DBSCAN은 클러스터링 알고리즘 중 하나입니다. 밀도 방식의 알고리즘을 사용해 클러스터링 합니다. K-means 클러스터링의 경우 거리 기반의 클러스터링 방식입니다. 밀도 기반의 클러스터링은 데이터의 밀도가 높은 부분을 클러스터링 하는 방식입니다.

DBSCAN 작동 원리

DBSCAN의 원리에 대해서 설명하도록 하겠습니다. 조대협님의 블로그에서 사진과 설명을 많이 참고했습니다. 출처

중요한 용어들입니다.

• 거리 e (epsilon)
• 점 m (min_points)
• 중심점 (core point)
• 경계점 (boder point)
• noise point (outlier)

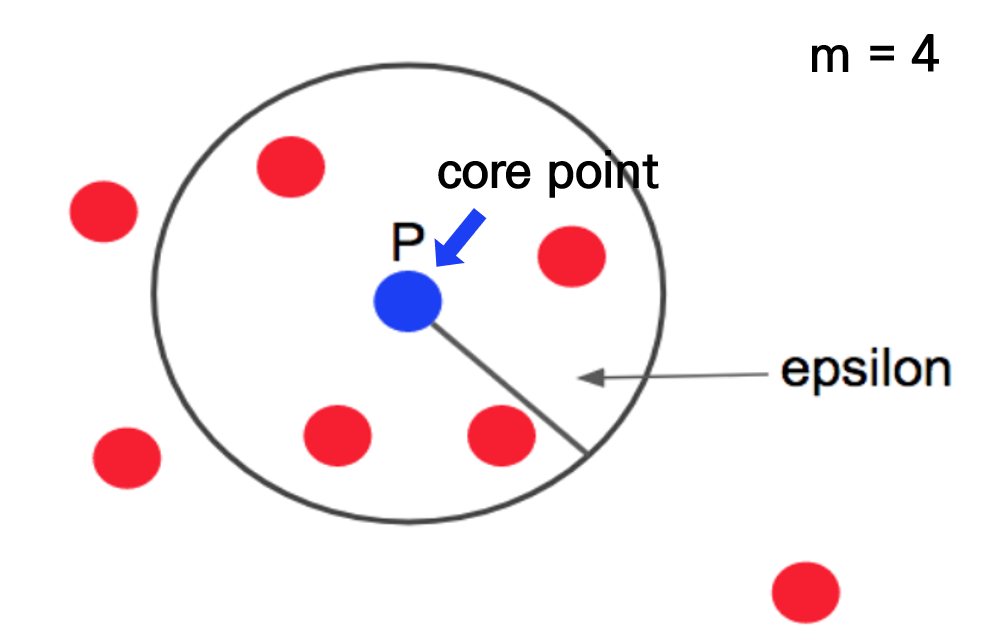
아래 그림과 같이 점 p가있다고 할 때, 점 p에서부터 거리 e내에 점이 m개있으면 하나의 군집이 됩니다. m은 4이므로, 점 p에서부터 반경내에 점들이 4개이상 있으므로 군집이 성립됩니다. 파란점 p는 중심점(core point)가 됩니다. 출처

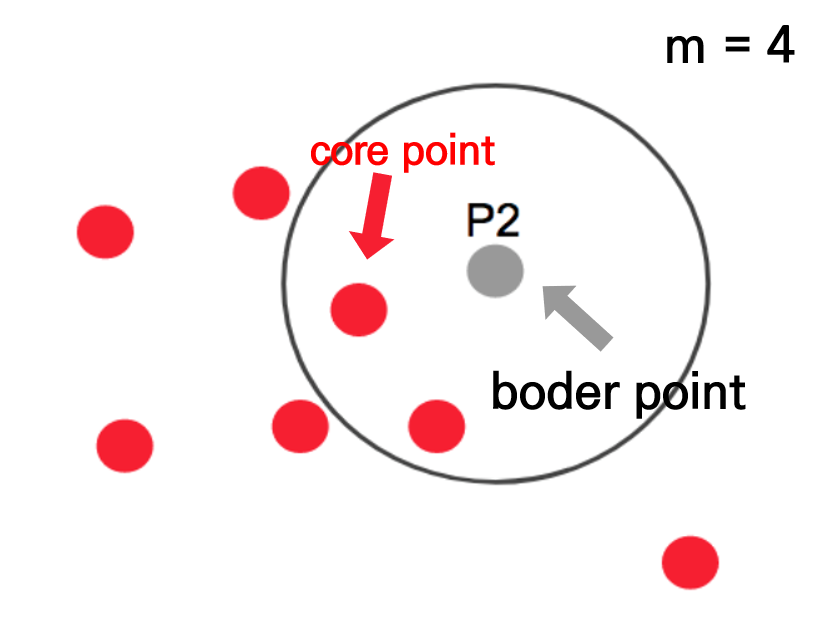
아래 그림에서 반경내에 점이 3개이기 때문에 core point은 되지 못하지만, core point의 군집에는 속하기 때문에 점 p2는 경계점(border point)이 됩니다. 출처

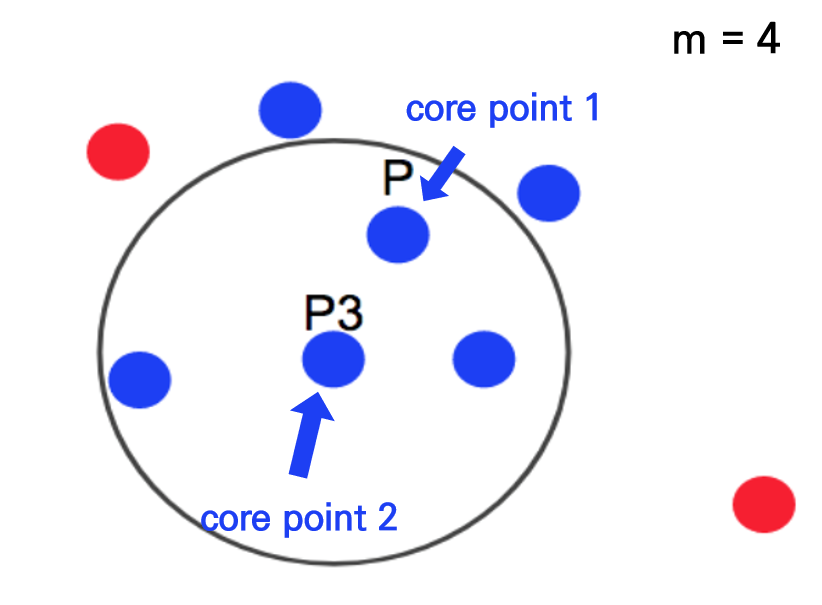
아래 그림에서 점 p3는 반경내에 점 4개를 가지고 있기 때문에 군집이 형성되고, 점 p3는 core point가 됩니다. 출처

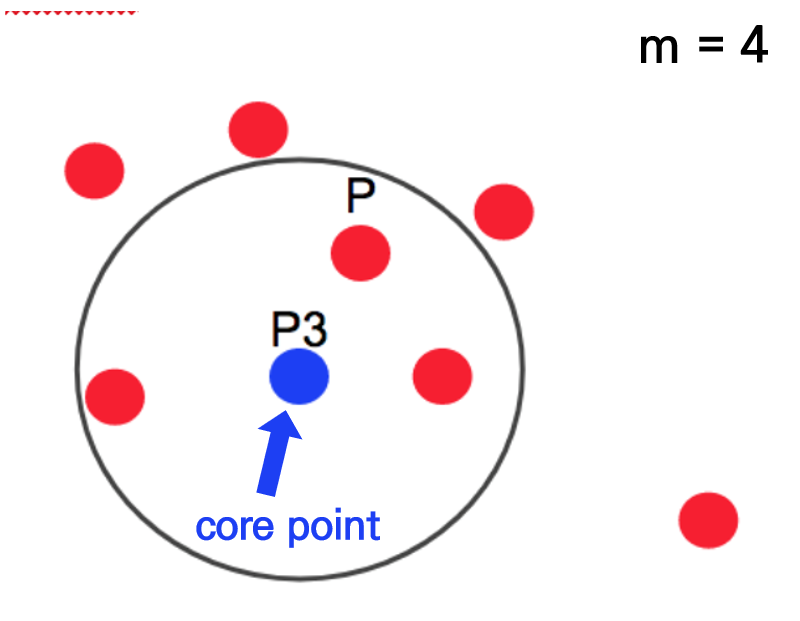
하지만, 점 p3를 중심으로 하는 반경내에 다른 core point p가 포함되어 있습니다. 이런 경우 core point p와 p3는 연결되어 있다고 보고, 하나의 군집으로 묶이게 됩니다. 출처

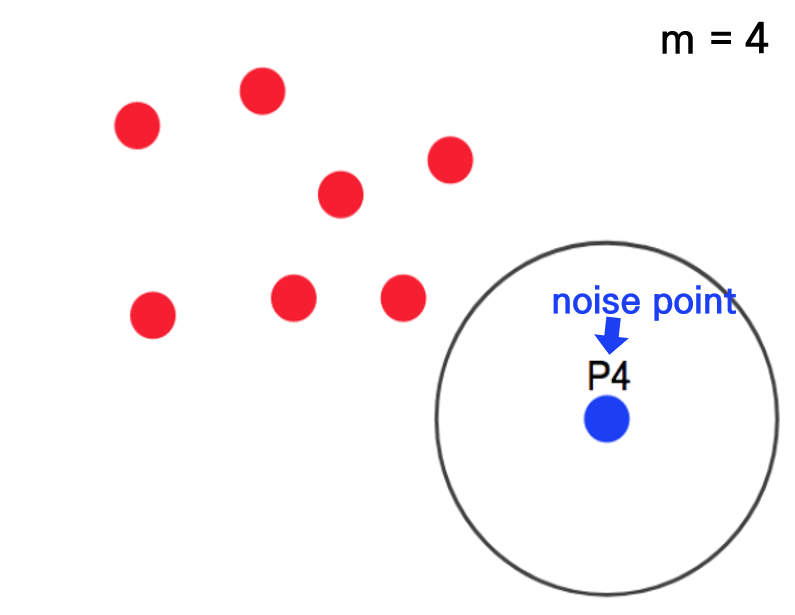
점 P4는 반경내에 점이 4개가 없으므로, 즉 어느 군집에도 속하지 않으므로 outlier가 됩니다. Outlier는 noise point라고 합니다. 출처

위 내용을 모두 정리하면 아래의 그림이 될 것 같습니다. 출처

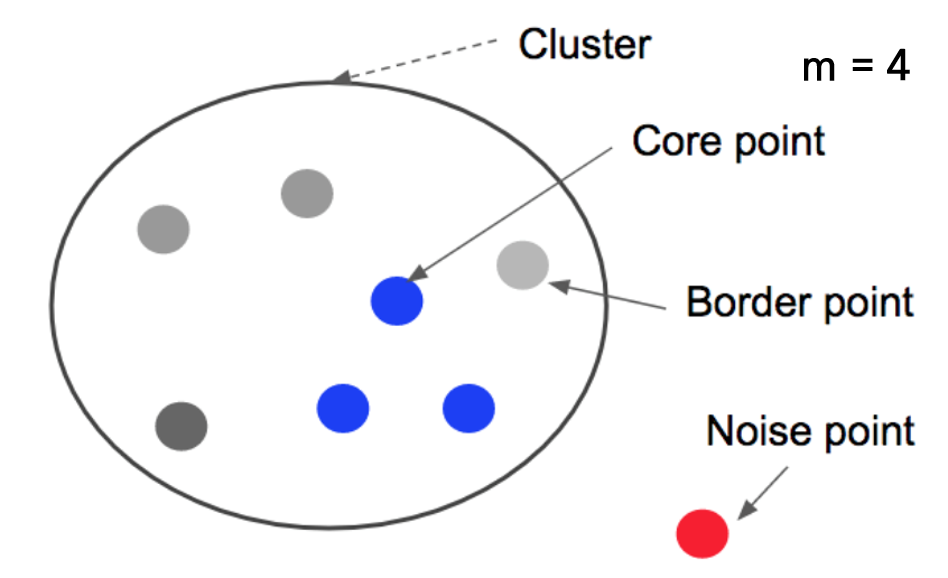
요악하자면, 점을 중심으로 epsilon 반경내에 m이상수의 점이 있으면 그 점을 중심으로 군집을 하게 됩니다. Core point가 서로 다른 core point의 군집의 일부가 되며느 두 군집은 하나의 군집으로 연결됩니다.

군집에는 속하지만 스스로 core point가 안되는 점을 border point라고 합니다. 어느 군집에도 속하지 않은 점은 outlier 즉, noise point라고 합니다.

DBSCAN 적용 방안

DBSCAN은 Point Anomaly를 찾을 때 유용합니다. 데이터를 밀도 기반으로 클러스터링 하는 방식이기 때문에, K-means처럼 클러스터의 개수를 정해줄 필요도 없습니다.

Anomaly Point를 감지하고 싶을 경우엔 DBSCAN과 같은 클러스터링 기법이 효율적일 수 있습니다. 시계열 데이터에서도, 범주형(categorical)데이터는 클러스터링 기법이 잘 작동할 수 있습니다.

Raw 데이터를 사용하는 것 보다는, 시계열 데이터일 경우 대표 값(평균, 최대, 최소 등)을 추출해 추출한 대표 값을 이용해 클러스터링한 후 noise point들을 찾는 방안도 있습니다.

다양한 클러스터링 모델들을 scikit-learn에서 제공해주고 있습니다. 쉽고 빠르게 본인의 데이터에 적용할 수 있습니다.